Zmiany nieliniowe

Kolejną sytuacją, z którą możemy mieć do czynienia to parametr, którego zależność od czasu nie jest liniowa. Przykładem takiego trendu może być zanieczyszczenie, którego wartość w początkowej fazie szybko rośnie a następnie ulega nasyceniu. Często odpowiednim podejściem jest zastosowanie transformacji logarytmicznej na osi czasu, co pozwoli dla tak przekształconych danych uzyskać zależność liniową i wykonywać dalsze analizy na danych przekształconych do postaci liniowej.

Po procesie linearyzacji możemy więc wykorzystać techniki analizy takie jak w przypadku zależności liniowej, tylko dla danych przekształconych. Możemy oceniać np. różnicę nachyleń trendu, czy też zastosować opisaną dalej kartę kontrolną regresji. Typowa nieliniowa zależność jest przedstawiona na rysunku 3. Różnica polegać będzie na interpretacji wyników, które teraz na osi czasu mają inną skalę, więc po wykonaniu analizy, należy powrócić do „naturalnej” osi czasu aby odpowiednio zinterpretować wynik analizy, a co za tym idzie poprawnie ocenić wystąpienie ewentualnego zdarzenia OOT.

Rys. 3 Przykład złego dopasowania zależności liniowej do danych zmieniających się w sposób nieliniowy

 

Karta kontrolna regresji

W przypadku, kiedy rozważany parametr z natury zmienia się liniowo w czasie, w zastosowanej analizie należy uwzględnić tę cechę. Innymi słowy zastosowana analiza musi ignorować naturalny trend parametru i skupić się na ewentualnym odejściu od tego wzorca. Funkcję taką może spełnić karta kontrolna regresji, która jest budowana podobnie jak zwykła karta kontrolna ale z tą różnicą, że linia centralna „podąża” za naturalnym trendem (jest to prosta regresji) i w oparciu o nią tworzone są linie kontrolne, w których powinny być zawarte wyniki jeżeli nie ma sygnału OOT. Przykład takiej karty prezentuje rysunek 4. Zauważmy, że karta może być zastosowana zarówno do rzeczywistych danych, które charakteryzują się zmiennością liniową jak i takich, dla których zmienność jest nieliniowa ale zostały odpowiednio przekształcone.

Dodatkowo, posługując się tego typu analizą, można oprócz samego wykrywania OOT oszacować prawdopodobieństwo przekroczenia przez badany parametr limitu, przed założonym terminem ważności [rys. 4]. Dzięki temu osoby analizujące jakość, dostają informację np. o zmianie takiego ryzyka po wprowadzeniu zmian w procesie. Można to oszacować obliczając odległość linii regresji w jednostkach σ (miary zmienności parametru wokół prostej), a następnie przenosząc to na wartość prawdopodobieństwa w oparciu o rozkład Gaussa.

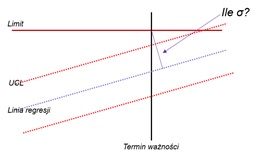
Rys. 4 Przykładowy układ karty kontrolnej regresji

 

Zakresy zmienności

Nie wszystkie parametry można zamodelować w postaci prostej regresji liniowej, nawet po przekształceniu i wtedy rozsądną metodą identyfikacji zmiany takiego parametru może być podejście „inżynierskie” oparte na danych. Załóżmy, że parametr ma skomplikowaną zależność związaną z czasem i próba odtworzenia tej zależności równaniami matematycznymi, wprowadzi tylko dodatkową niepewność do procesu oceny odejścia od trendu. I tak w przypadku badań stabilności można potraktować każdy punkt czasowy jako oddzielny element do analizy i weryfikować, czy nowe dane w kolejnym punkcie nie przekraczają wyznaczonych dla tego konkretnego punktu granic (zakresu).

Opracowując wzorzec (granice) dla takiego parametru musimy skorzystać z technik statystycznych i wyznaczyć zakres parametru w każdym punkcie opierając się oczywiście na dostępnych danych historycznych. Po wyznaczeniu poszczególnych zakresów możemy je potraktować jako wspólny „kanał” [rys. 5], w którym w przyszłości powinny znaleźć się poprawne wyniki pomiarów. Następnie po prostu każdą nowo otrzymaną wartość porównujemy, czy mieści się w określonym przedziale dla danego punktu, a każde wyjście poza ten zakres będzie traktowane jako odejście od trendu.

Rys. 5. Przebieg zakresu wartości